Grammatical Evolution in HeuristicLab
The latest version of HeuristicLab now also includes a plugin for grammatical evolution (GE)! The plugin has been implemented by Sabine Winkler for her Bachelor's thesis, and she kindly contributed her implementation to HeuristicLab, so that we could integrate it into the stable development branch.
So far, the implementation supports two problems: symbolic regression and the artifical ant problem for the Santa Fe trail. However, additional problem types for grammatical evolution can be added easily in a similar way as for tree-based GP (see our documentation on implementing GP problems)
The implementation of GE reuses existing classes and methods for tree-based GP and acts mainly as a translator between the integer vector encoding and the tree encoding. In the mapping process the grammar is used to build a tree from the integer vector. The concept of the mapping process is shown in the following diagram:
The GE plugin also provides different multiple variants of mappers that have been described in literature including depth-first, breath-first, and the π-GE mappers. In GE the genotype to phenotype mappers use a grammar to create a tree from an integer vector. The elements of the integer vector are read from left to right and the tree is built starting from the root symbol of the grammar. For each non-terminal symbol the mapper reads one element from the vector and chooses the alternative for extending the tree based on this value. An example for the depth-first mapper is shown in the following figure.
In GE the genotype to phenotype mapping is prone to the so-called ripple-effect which describes the phenomenon that a small change of the integer-vector might lead to a completely different tree after mapping. This hampers the search process and could lead to premature convergence of the algorithm.
We are happy about contributions to the grammatical evolution implementation or to HeuristicLab in general. So, if you have implemented an algorithm or problem or even only a custom operator feel free to contribute!
Figures (C) Sabine Winkler, with kind permission.
New Video Tutorials
Dear HeuristicLab Users!
We have spent two days of intensive work in the solitude of northern Mühlviertel and prepared several new video tutorials for HeuristicLab. The videos are already available in our youtube channel.
Additionally, we prepared a major overhaul of the HeuristicLab website to improve the user experience and access to the documentation. The new website will go online in the next few days.
The new tutorials:
- How to create user defined problems (n-queens)
- How to use HeuristicLab Hive
- Rapid prototyping using the scripting environment
- Symbolic classification with HeuristicLab
- Symbolic regression with HeuristicLab
Gaussian Processes for Regression and Classification
With the latest HeuristicLab version 3.3.8 we released an implementation of Gaussian process models for regression analysis. Our purely managed C# implementation is mainly based on the MATLAB implementation by Rasmussen and Nickisch accompanying the book "Gaussian Processes for Machine Learning" by Rasmussen and Williams (available online).
If you want to try Gaussian process regression in HeuristicLab, simply open the preconfigured sample. You can also import a CSV file with your own data.
The Gaussian process model can be viewed as a Bayesian prior distribution over functions and is related to Bayesian linear regression.
Samples from two different one-dimensional Gaussian processes:
Similarily to other models, such as the SVM, the GP model also uses the 'kernel-trick' to handle high-dimensional non-linear projections to feature space efficiently.
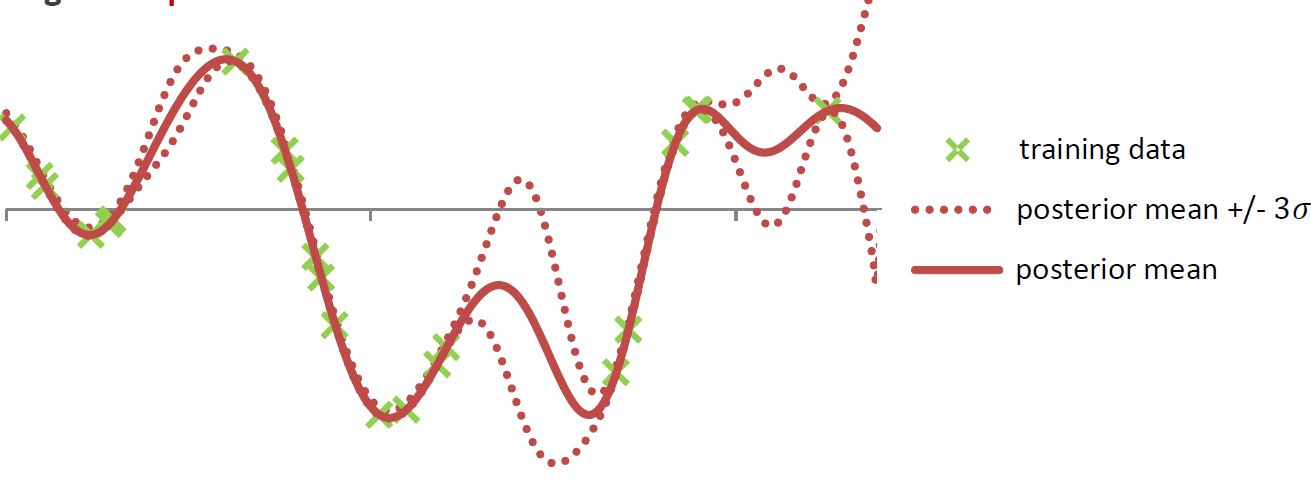
'Fitting' the model means to calculate the posterior Gaussian process distribution by conditioning the GP prior distribution on the observed data points in the training set. This leads to a posterior distribution in which functions that go through the observed training points are more likely. From the posterior GP distribution it is easily possible to calculate the posterior predictive distribution. So, instead of a simple point prediction for each test point it is possible to use the mean of the predictve distribution and calculate confidence intervals for the prediction at each test point.
The model is non-parametric and is fully specified via a mean function and a covariance function. The mean and covariance function often have hyper-parameters that have to be optimized to fit the model to a given training data set. For more information check out the book.
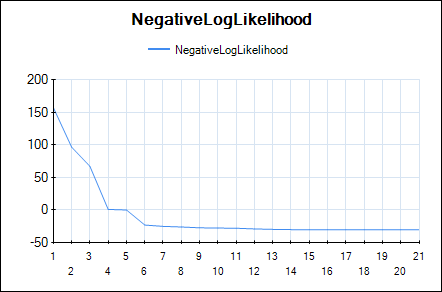
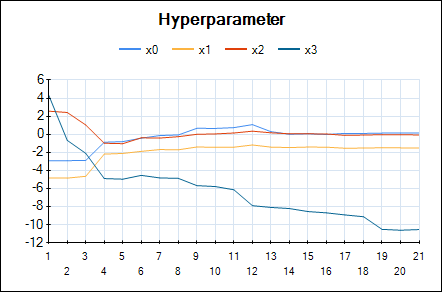
In HeuristicLab hyper-parameters of the mean and covariance functions are optimized w.r.t. the likelihood function (type-II ML) using the gradient-based BFGS algorithm. In the GUI you can observe the development of the likelihood and the values of the hyper-parameters over BFGS iterations. The output of the final Gaussian process model can also be visualized using a line chart that shows the mean prediction and the 95% confidence intervals.
Line chart of the negative log-likelihood:
Line chart of the optimized hyper-parameters:
Output of the model (mean and confidence interval):
We observed Gaussian process models often produce very accurate predictions, especially for low-dimensional data sets with up to 5000 training points. For larger data sets the computational effort becomes prohibitive (we have not yet implemented sparse approximations).
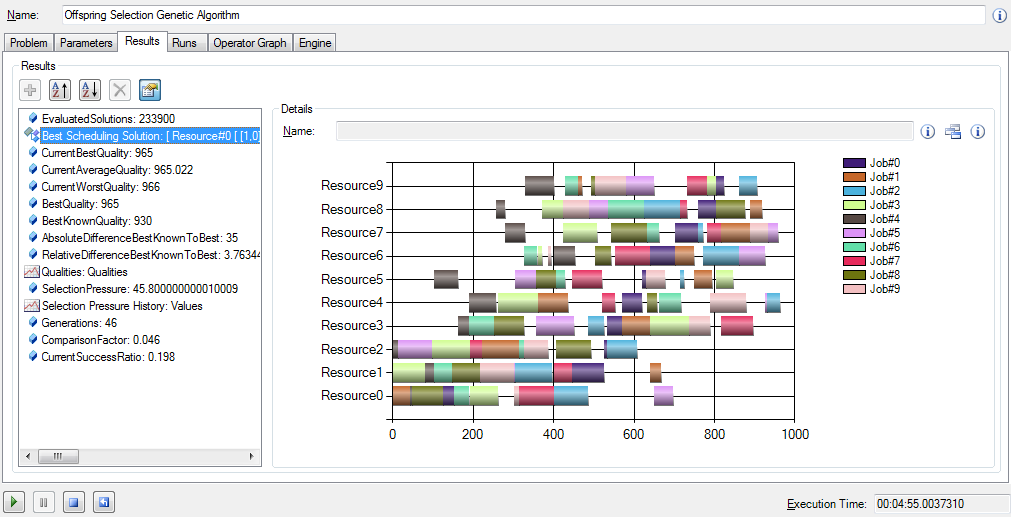
Job Shop Scheduling Add-on for HeuristicLab
Joseph Helm finished a very nice implementation of the job shop scheduling problem (JSSP) earlier this year. The add-on is available as zip-archive from our add-ons daily builds download page. Just extract the .dll-files in the zip-archive into your HeuristicLab installation directory and you are ready to create and optimize JSSP instances.
EDIT: The JSSP implementation is included in the regular HeuristicLab releases since HeuristicLab 3.3.8.
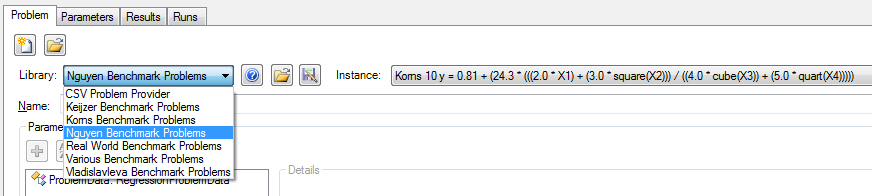
Symbolic Regression Benchmark Functions
At last year's GECCO in Dublin a discussion revolved around the fact that the genetic programming community needs a set of suitable benchmark problems. Many experiments presented in the GP literature are based on very simple toy problems and thus the results are often unconvincing. The whole topic is summarized on http://gpbenchmarks.org.
This page also lists benchmark problems for symbolic regression from a number of different papers. Thanks to our new developer Stefan Forstenlechner most of these problems are now available in HeuristicLab and will be included in the next release. The benchmark problems can be easily loaded directly in the GUI through problem instance providers. Additionally, it is very simple to create an experiment to execute an algorithm on all instances using the new 'Create Experiment' dialog implemented by Andreas (see the previous blog post)
I used these new features to quickly apply a random forest regression algorithm (R=0.7, Number of trees=50) on all regression benchmark problems and got the following results. Let's see how symbolic regression with GP will perform...
| Problem instance | Avg. R² (test) |
| Keijzer 4 f(x) = 0.3 * x *sin(2 * PI * x) | 0.984 |
| Keijzer 5 f(x) = x ^ 3 * exp(-x) * cos(x) * sin(x) * (sin(x) ^ 2 * cos(x) - 1) | 1.000 |
| Keijzer 6 f(x) = (30 * x * z) / ((x - 10) * y^2) | 0.956 |
| Keijzer 7 f(x) = Sum(1 / i) From 1 to X | 0.911 |
| Keijzer 8 f(x) = log(x) | 1.000 |
| Keijzer 9 f(x) = sqrt(x) | 1.000 |
| Keijzer 11 f(x, y) = x ^ y | 0.957 |
| Keijzer 12 f(x, y) = xy + sin((x - 1)(y - 1)) | 0.267 |
| Keijzer 13 f(x, y) = x^4 - x^3 + y^2 / 2 - y | 0.610 |
| Keijzer 14 f(x, y) = 6 * sin(x) * cos(y) | 0.321 |
| Keijzer 15 f(x, y) = 8 / (2 + x^2 + y^2) | 0.484 |
| Keijzer 16 f(x, y) = x^3 / 5 + y^3 / 2 - y - x | 0.599 |
| Korns 1 y = 1.57 + (24.3 * X3) | 0.998 |
| Korns 2 y = 0.23 + (14.2 * ((X3 + X1) / (3.0 * X4))) | 0.009 |
| Korns 3 y = -5.41 + (4.9 * (((X3 - X0) + (X1 / X4)) / (3 * X4))) | 0.023 |
| Korns 4 y = -2.3 + (0.13 * sin(X2)) | 0.384 |
| Korns 5 y = 3.0 + (2.13 * log(X4)) | 0.977 |
| Korns 6 y = 1.3 + (0.13 * sqrt(X0)) | 0.997 |
| Korns 7 y = 213.80940889 - (213.80940889 * exp(-0.54723748542 * X0)) | 0.000 |
| Korns 8 y = 6.87 + (11 * sqrt(7.23 * X0 * X3 * X4)) | 0.993 |
| Korns 9 y = ((sqrt(X0) / log(X1)) * (exp(X2) / square(X3))) | 0.000 |
| Korns 10 y = 0.81 + (24.3 * (((2.0 * X1) + (3.0 * square(X2))) / ((4.0 * cube(X3)) + (5.0 * quart(X4))))) | 0.003 |
| Korns 11 y = 6.87 + (11 * cos(7.23 * X0 * X0 * X0)) | 0.000 |
| Korns 12 y = 2.0 - (2.1 * (cos(9.8 * X0) * sin(1.3 * X4))) | 0.001 |
| Korns 13 y = 32.0 - (3.0 * ((tan(X0) / tan(X1)) * (tan(X2) / tan(X3)))) | 0.000 |
| Korns 14 y = 22.0 + (4.2 * ((cos(X0) - tan(X1)) * (tanh(X2) / sin(X3)))) | 0.000 |
| Korns 15 y = 12.0 - (6.0 * ((tan(X0) / exp(X1)) * (log(X2) - tan(X3)))) | 0.000 |
| Nguyen F1 = x^3 + x^2 + x | 0.944 |
| Nguyen F2 = x^4 + x^3 + x^2 + x | 0.992 |
| Nguyen F3 = x^5 + x^4 + x^3 + x^2 + x | 0.983 |
| Nguyen F4 = x^6 + x^5 + x^4 + x^3 + x^2 + x | 0.960 |
| Nguyen F5 = sin(x^2)cos(x) - 1 | 0.975 |
| Nguyen F6 = sin(x) + sin(x + x^2) | 0.997 |
| Nguyen F7 = log(x + 1) + log(x^2 + 1) | 0.977 |
| Nguyen F8 = Sqrt(x) | 0.966 |
| Nguyen F9 = sin(x) + sin(y^2) | 0.988 |
| Nguyen F10 = 2sin(x)cos(y) | 0.986 |
| Nguyen F11 = x^y | 0.961 |
| Nguyen F12 = x^4 - x^3 + y^2/2 - y | 0.979 |
| Spatial co-evolution F(x,y) = 1/(1+power(x,-4)) + 1/(1+pow(y,-4)) | 0.983 |
| TowerData | 0.972 |
| Vladislavleva Kotanchek | 0.854 |
| Vladislavleva RatPol2D | 0.785 |
| Vladislavleva RatPol3D | 0.795 |
| Vladislavleva Ripple | 0.951 |
| Vladislavleva Salutowicz | 0.996 |
| Vladislavleva Salutowicz2D | 0.960 |
| Vladislavleva UBall5D | 0.892 |
Math notation for symbolic models
In February I have a little more time available that I can spend on HeuristicLab development. So I implemented a new view that shows genetic programming solutions for symbolic data analysis problems in conventional math notation. This has been on our wishlist for a long time, however, up to now we didn't see a good way of implementing this. The implementation is not ideal because it relies on the MathJax library (Javascript) to display the models in a webbrowser control. Using the daily build of the trunk version you can try this new feature. I hope you find it useful.
Financial Analysis with HeuristicLab
One application that I've been interested in lately is financial analysis.
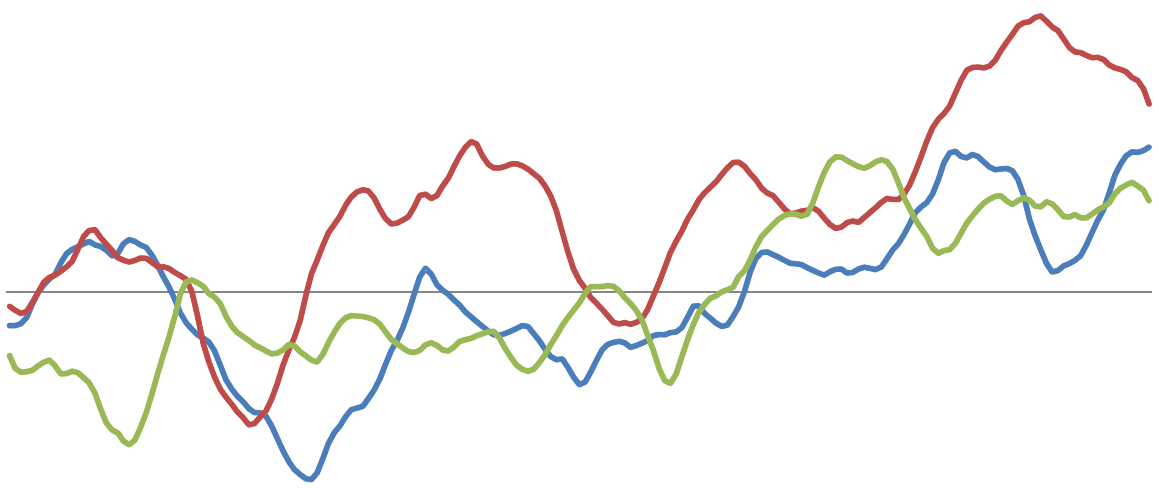
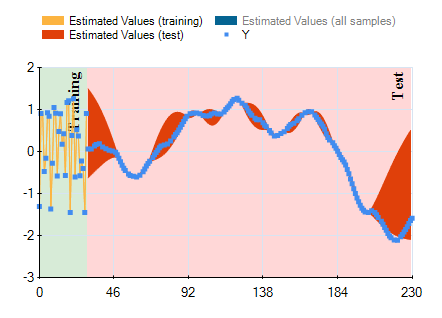
Recently I've looked at interest rate swaps in more detail. Interest rate swaps are an important financial instrument for controlling risk, but are also used for speculative purposes. Using the genetic programming capabilities of HeuristicLab it is relatively easy to generate a regression model to estimate the interest rate swap yield. The result for the European 10-year interest rate swap (monthly data) in the time span from April 1991 until August 2011 can be seen in the next figure.
In the last section from index 582 onwards (July 2007 - August 2011) the output of the model (red line) deviates very strongly from the actually observed values.
To get a better idea of the underlying relations found by GP it is interesting to study variable impacts. The most important variables for the 10-year European interest rate swap yield found through the genetic programming runs are:
| Most relevant variables | Hold out set |
|---|---|
| US M1, US Mortgage Market Index | March 1991 - April 1995 |
| Eurozone Employment qq, US M1, US Corporate Profits | April 1995 - May 1999 |
| US Corporate Profits, Eurozone Employment qq, US U Michigan Expectations Prelim. | May 1999 - June 2003 |
| US Corporate Profits, Eurozone Employment qq | June 2003 - July 2007 |
| US Existing Home Sales | July 2007 - August 2008 |
Interestingly the most important variables differ for different time spans. Only the corporate profits and the number of employed persons in the Euro zone are detected as relevant over a larger time span.
The following table shows the variable impact calculation results for the first fold in greater detail. It can be clearly seen that money supply M1 in the US and the US mortgage market index are used repeatedly in all models. This is a strong indicator that there is a strong correlation of these variables and the interest rate swap yield for the time span from April 1995 until August 2011 which was used as training set for these models. As can be seen in the previous chart the output on the hold out set (March 1991 - April 1995) is relatively accurate.

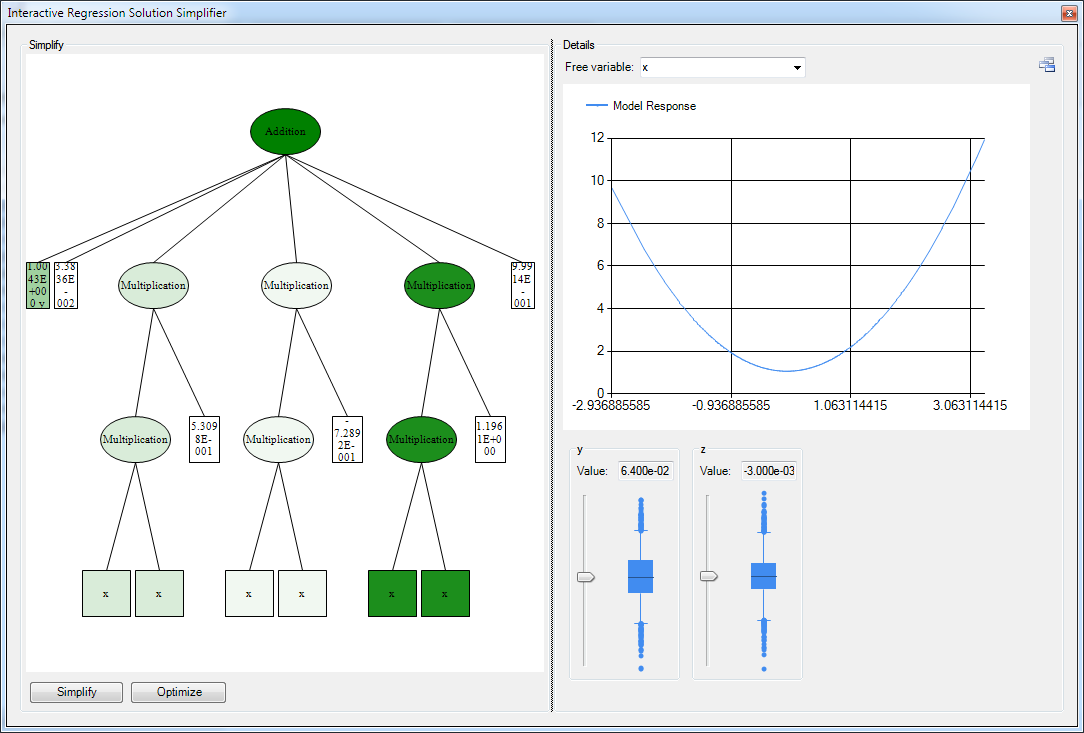
New Feature for System Identification: Model Response View
Last week I implemented a new view for symbolic regression models that makes it possible to analyse the impact of a given input variable on the output of the model in more detail. I'm already looking forward to apply it to real world scenarios.
The development efforts for this feature are tracked in ticket #1621

 rss
rss