Particle Swarm Optimization

Particle swarm optimization (PSO) is a stochastic population-based optimization algorithm that was first introduced by Kennedy and Eberhart. Members of the population (= swarm) are called particles. Each particle moves around in the search space, taking advantage of the particle’s own experience and the experience of the particle’s neighbours or of the whole swarm to guide the search. A great introduction to PSOs can be found in (Kennedy and Eberhart, 2001).

Our particle swarm optimization algorithm has been designed to work with arbitrary solution encodings. However, so far a concrete implementation is only available for real vector encoded problems, i.e. Single Objective Test Function.

Algorithm Parameters:

Parameter	Description
Analyzer	The operator used to analyze each generation.
Inertia	Inertia weight on a particle's movement (omega). Default: -0.2
InertiaUpdater	Updates the omega parameter.
MaxIterations	The maximum number of iterations which should be processed. Default: 1000
MutationProbability	The probability that the mutation operator is applied on a solution.
Mutator	The operator used to mutate solutions.
NeighborBestAttraction	Weight for pull towards the neighborhood best solution or global best solution in case of a totally connected topology (phi_g). Default: 3.7
ParticleCreator	Operator creates a new particle.
ParticleUpdater	Operator that updates a particle.
PersonalBestAttraction	Weight for particle's pull towards its personal best soution (phi_p). Default: -0.01
Population Size	The size of the population of solutions.
Seed	The random seed used to initialize the new pseudo random number generator. Default: 0
SetSeedRandomly	True if the random seed should be set to a random value, otherwise false. Default: true
SwarmSize	Size of the particle swarm. Default: 10
SwarmUpdater	Encoding-specific parameter which is provided by the problem. May provide additional encoding-specific parameters, such as velocity bounds for real valued problems.
TopologyInitializer	Creates neighborhood description vectors.
TopologyUpdater	Updates the neighborhood description vectors.

Local vs. Global PSO

In the (standard) global PSO, all the particles are neighbors of each other (= fully connected topology). Therefore the position of the global best particle is propagated to the whole swarm and affects the velocity update. If the current global optimum is not close to the best solution, it may become impossible for the swarm to explore other areas of the search space. Generally speaking, global PSOs usually converge faster and get trapped in local optima more easily.

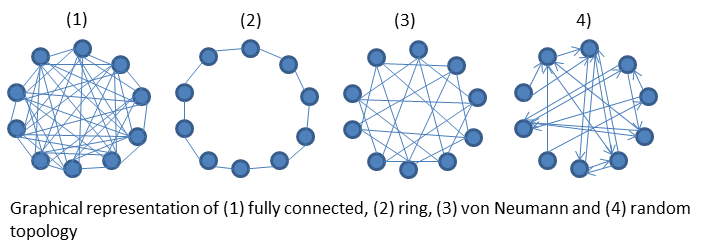
In local PSO variants, particles are grouped into neighborhoods according to a certain strategy. In this variant only the neighbor particles of a given particle can influence its velocity update. Consequently, local PSOs (with topologies) converge slower than global PSOs but are less likely to be captured in local minima due to greater population diversity. An overview of the topologies available in HeuristicLab is depicted in the picture below:

The fully connected topology is the standard configuration (= global PSO). If you wish to use another topogly you have to set the TopologyInitializer parameter to one of the following:

• RandomTopologyInitializer: Randomly connectes every particle with NroOfParticles other particles. Neighborhood connections are not symmetric, meaning if particle A is a neighbor of particle B, particle B does not necessarily have to be a neighbor of particle A. The default NroOfParticles is 3. The picture above shows a random neighborhood with NroOfParticles=2.
• RingTopologyInitializer: Every particle is connected with its preceeding and its following particle.
• VonNeumannTopologyInitializer: Every particle is connected with 4 other particles, the two following and the two previous, wrapping around at the beginning and the end of the population.

(Kennedy and Mendes, 2002) and - in more detail - (Mendes, 2004) investigated the impact of different topologies on algorithm performance. They found that the global PSO was quick to converge but yielded the worst results. Circular and weel topologies improved the results moderately and using the Von Neumann topology produed the best results.

The topologies are static and do not change during algorithm execution, once they have been initialized. If you want to implement your own topology, you must inherit from ITopologyInitializer or derive from the base class TopologyInitializer.

Parameter Tuning

Like many other metheuristics, the PSO algorithm frequently faces the problem of being trapped in local optima. Balancing the global exploration and local exploitation abilities of PSO is therefore very important. Tweaking the following PSO parameters for your problem (or even instance) can yield better results:

Velocity Bounds One crucial parameter is the minimum/maximum velocity bounds vector. Particle velocities on each dimension are clamped to a certain velocity range by the parameter VelocityBounds. Therefore VelocityBounds affects the maximum global exploration ability of PSO, since

• large velocity --> global exploration and
• small velocity --> local exploitation.

Inertia Weight The inertia weight parameter was introduced in (Shi and Eberhart, 1998)). It was soon discovered that decreasing inertia weight over time can further improve results as dicussed in (Shi and Eberhart, 1999)). Other researchers have since experimented with dynamic adjustment of inertia weight, for instance via fuzzy optimization, by linear decreasing or increasing or randomizing the parameter.

Also, a recent paper by (Pedersen 2010) provides a most helpful table of PSO parameter settings that have been tuned via meta/optimization for different optimization scenarios. We recommend them as a first starting point when optimizing new problems. Some of the settings (like using a negative inertia weight and personal attraction weight) may seem quirky, but we also got some very good results with those settings.

Dynamic Parameters

As mentioned in the previous section it has been found to be benefitial to adjust parameters dynamically during runtime. Currently you can enable dynamic parameter modification for the following two parameters.

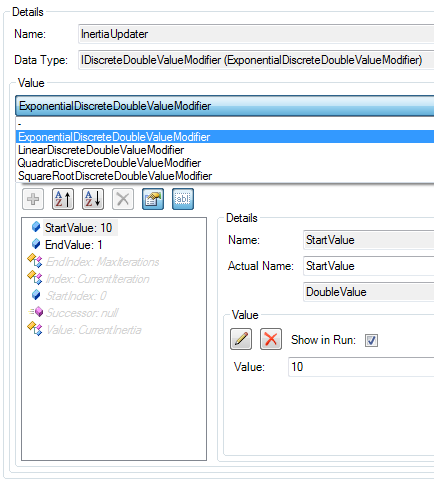
• Inertia Weight: Configure the InertiaUpdater to adjust the inertia weight. You can select any operator that implements IDiscreteDoubleValueModifier. The standard Simulated Annealing annealing operators (exponential, square root, linear, quadratic increase/decrease) can be used as shown in the screenshot below. You only have to select an appropriate annealing operator and set a desired StartValue and EndValue. Please note that some additional parameters of the operator are hidden, among them the StartIndex, Index and EndIndex. Those are set by default to cover the whole algorithm execution time from iteration 0 to MaxIterations.

Tip: You can show hidden parameters by clicking on the Show hidden parameters button.

• Velocity Bounds: In the SwarmUpdater the velocity bounds vector can be likewise adjusted. You can either adjust it statically by altering the VelocityBounds parameter. Or you can select an IDiscreteDoubleValueModifier that will set all vector dimensions equally (symmetric around zero). In addition, you have to set the VelocityBoundsStartValue and VelocityBoundsEndValue. Note that VelocityBoundsStartIndex, VelocityBoundsIndex and VelocityBoundsEndIndex are once again hidden (but can be un-hidden and changed manually, if you wish). The parameters are propagated to the IDiscreteDoubleValueModifier so there is no need to paramiterize it as well.

Topology Updaters

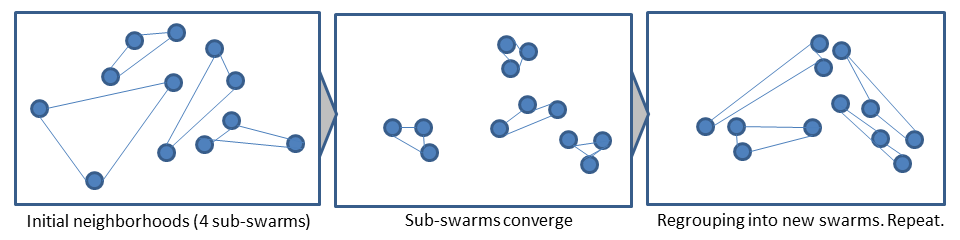
• MultiPSOTopologyUpdater: The whole population is divided into NrOfSwarms non-overlapping sub-swarms. Neighborhood topology is dynamic and randomly assigned. Swarms are re-grouped every regroupingPeriod iteration. The operator is implemented as described in (Liang and Suganthan 2005).

Is there a sample/tutorial?

A global PSO with dynamically updated inertia and velocity bounds has been implemented for the Schwefel test function. Details and parameter settings:

Particle Swarm Optimization + Schwefel Test Function

References:

• Kennedy, J. and Eberhart, R.C., 2001. Swarm Intelligence. Morgan Kaufmann. ISBN 1-55860-595-9.
• Kennedy, J. and Mendes, R. 2002. Population structure and particle swarm performance. Congress on Evolutionary Computation, pp. 1671-1676.
• Liang, J.J. and Suganthan, P.N., 2005. Dynamic multi-swarm particle swarm optimizer. IEEE Swarm Intelligence Symposium, pp. 124-129.
• Pedersen, M.E.H., 2010. ​| Good parameters for particle swarm optimization. Technical Report HL1001 (Hvass Laboratories)
• Mendes, R., 2004. Population Topologies and Their Influence in Particle Swarm Performance, PhD thesis, Universidade do Minho.
• Shi, Y. and Eberhart, R.C., 1998. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, pp. 69–73, IEEE Press.
• Shi, Y. and Eberhart, R.C., 1999. Empirical study of particle swarm optimization. In Proceedings of the 1999 IEEE Congress on Evolutionary Computation, pp. 1945–1950, IEEE Press.