| Version 3 (modified by gkronber, 13 years ago) (diff) |
|---|
Genetic Programming with HeuristicLab
Samples for Genetic Programming
HeuristicLab supports tree-based (Koza-style) genetic programming. This classical form of genetic programming uses a tree-based representation of solution candidates. The data types and operators to work with tree-bsaed solution candidates are implemented in the plugin HeuristicLab.Encodings.SymbolicExpressionTree.
Supported operators (in 3.3.6):
- Full tree creator
- Grow tree creator
- Ramped-half-half tree creator
- Probabilistic tree creator (PTC)
- Subtree crossover
- Change node type manipulator (single point mutation, symbols)
- Replace branch manipulator (removes a branch and replaces it with a randomly initialized branch)
- One-point shaker (single point mutation, only parameters)
- Full-tree shaker (uniform mutation, only parameters)
Genetic Programming Tasks
The symbolic expression tree encoding contains the implementation of the problem independent data structure (a tree of symbols) and operators. Based on the encoding we implemented three well-known GP problems.
Supported Problems (in 3.3.6):
- Symbolic regression (HeuristicLab.Problems.DataAnalysis.Symbolic.Regression)
- Symbolic classification (HeuristicLab.Problems.DataAnalysis.Symbolic.Classification)
- Artificial Ant problem (HeuristicLab.Problems.ArtificialAnt)
Samples for all three of these problems are available on the start page in HeuristicLab. Additional samples are available here: http://dev.heuristiclab.com/trac/hl/core/wiki/UsersSamples#GeneticProgramming
Symbolic regression
Symbolic regression is a particular variant of data analysis. The goal is to find a functional expression of any form which estimates the values of a specified target variable (continuous) based on values of a set of input variables (discrete/continuous). It is thus similar to linear regression, however, in linear regression the structure of the model is predefined (linear combination of the input variables) and only the parameters for the model have to be estimated while in symbolic regression the structure of the model is unconstrained and the structure as well as the parameters have to be determined. This is a problem that can be solved by genetic programming.
The symbols that can be used in symbolic regression models is problem dependent. So these symbols (mathematical operators: +,-,/,* ... and operands: constants, variables) are implemented in the problem specific plugin HeuristicLab.Problems.DataAnalysis.Symbolic. Evaluators for these problem-specific instances of symbolic expression trees are also implemented in this plugin.
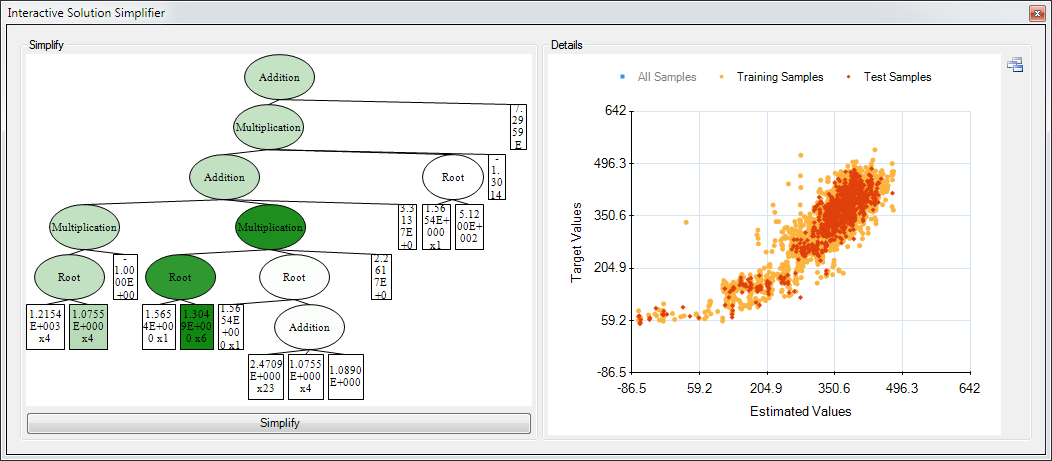
HeuristicLab provides many possibilities to analyse the resulting symbolic regression solutions. Some of them are shown in the screenshot.
Symbolic regression features:
- Tree visualization of models
- Large range of accuracy metrics: MSE, MAE, relative error, R², NMSE
- Visualization of model output: scatter plot, line chart, error characteristic curve
- Automatic simplification of models by transformation into a canonical form
- Visualization of the impact strength of branches
- Manual simplification (pruning)
- Model export for LaTeX publications
Symbolic classification
The goal in symbolic classification is to find a model that estimates the target class value (discrete) from the value of input variables (discrete, continuous). In our implementation the models for symbolic regression and symbolic classification can contain the same symbols (operators and operands). Thus we actually evolve a discriminating function for the classes and later any threshold value can be used to map the continuous output of the discriminating function to the actual class values.
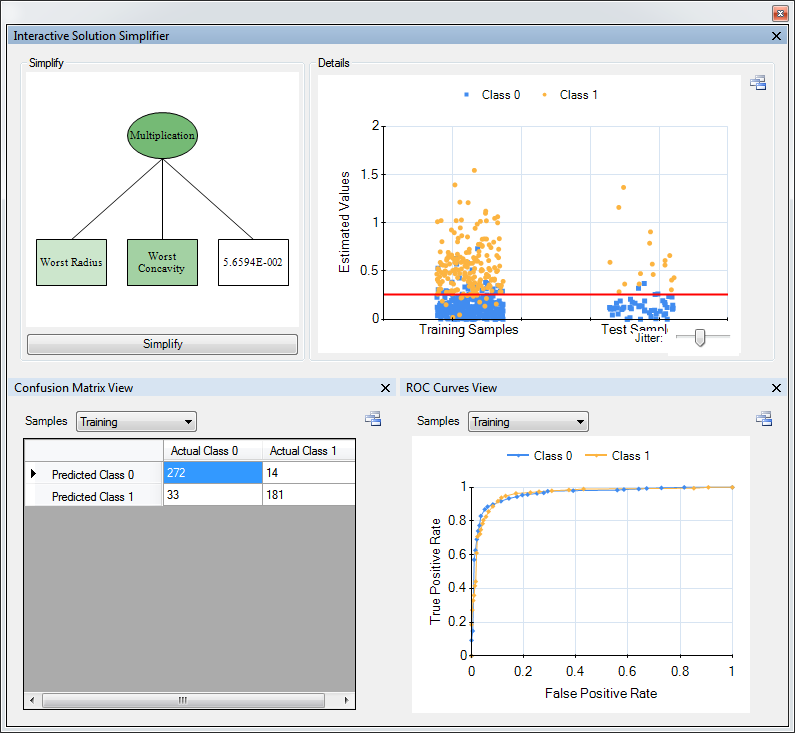
However, we provide a number of additional accuracy metrics and output visualizations that are useful for classification solutions. Some of them are shown in the screenshot on the right side.
Symbolic classification features:
- Classification specific accuracy metrics: accuracy, Gini coefficient, AUC,
- Visualization of model output: classification output with threshold, receiver operating characteristic curve
- Misclassification matrix
Of course the following features are also available for symbolic classification solutions:
- Tree visualization of models
- Automatic simplification of models by transformation into a canonical form
- Visualization of the impact strength of branches
- Manual simplification (pruning)
- Model export for LaTeX publications
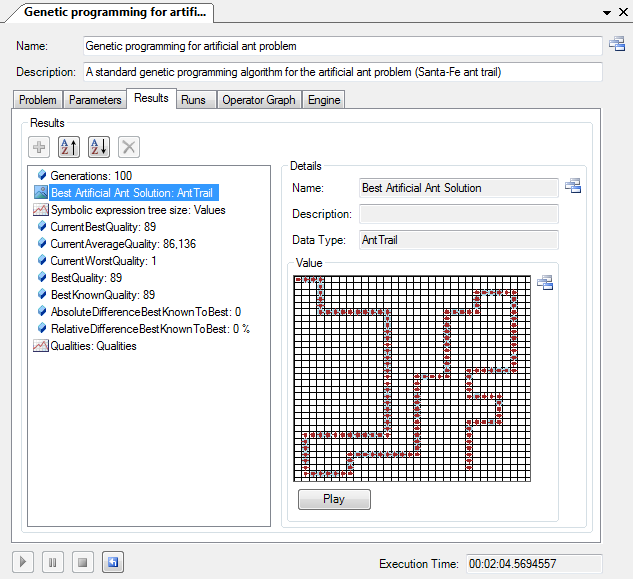
Artificial Ant
The artificial ant problem is a very simple implementation of a genetic programming problem. Right now we only provide the Santa-Fe ant trail as problem instance. The implementation of the artificial ant problem can be used as a reference implementation when you want to implement your own plugin for genetic programming. It shows how to define the problem-specific symbol set and a grammar which defines valid tree structures. It also contains a problem specific evaluator and solution visualization. On the right you can see the solution visualization for the artifical ant problem.
Algorithms for Genetic Programming
Because of the strict separation of the implementations of algorithms, problems, and encodings in HeuristicLab. It is possible to solve symbolic regression of symbolic classification problems with all population based algorithms using either a crossover or manipulation operator to evolve solutions. The algorithm that comes closest to the original formulation of genetic programming by Koza is the genetic algorithm.
Available algorithms for genetic programming:
- genetic algorithm
- evolution strategy
- island genetic algorithm
- offspring selection genetic algorithm (and even SASEGASA)
In the future we plan to implement move operators for the symbolic expression tree encoding. This would make it possible to solve genetic programming problems also with trajectory-based algorithms like tabu-search, particle swarm optimization, or variable neighborhood search.
Advanced Topics
Automatically Defined Functions (ADF)
We also provide an implementation for automatically defined functions (ADFs) as described by Koza. Automatically defined functions allow to extract useful code fragments into a separate function which can be called multiple times either while executing the result producing branch or another ADF. ADFs are created and manipulated by architecture altering operators while evolving genetic programming solutions. This means ADFs underlie selection pressure in the same way as the main result producing branch and the evolutionary process determines if ADFs survive in the final population and which code fragments are moved to ADFs.
Supported architecture altering operators (3.3.6)
- Subroutine creater
- Subroutine deleter
- Subrouting duplicater
- Argument creater
- Argument deleter
- Argument duplicater
Supporting ADFs fully and correctly is not easy and lead to many non-trivial changes in the data types and operators for symbolic expression trees.
Attachments (3)
- model_export1.png (158.4 KB) - added by gkronber 13 years ago.
- model_export2.png (139.2 KB) - added by gkronber 13 years ago.
- model_export3.png (127.2 KB) - added by gkronber 13 years ago.
Download all attachments as: .zip