Exact Optimization

Google OR-Tools

According to Google, "​OR-Tools is an open source software suite for optimization, tuned for tackling the world's toughest problems in vehicle routing, flows, integer and linear programming, and constraint programming." OR-Tools are available for C++, Python, Java and .NET, the latter API can be used in HeuristicLab.

OR-Tools includes solvers for

• Contraint Programming (​CP, ​CP-SAT),
• Linear and Mixed-Integer Programming (​BOP, ​Cbc, ​Clp, ​CPLEX, ​Glop, ​GLPK, ​Gurobi and ​SCIP),
• Routing,
• Scheduling and
• Network Flows.

For a complete overview, see ​https://developers.google.com/optimization/introduction/overview. You can use all solvers in HeuristicLab, just create a C# Script and make sure the ​Microsoft Visual C++ 2017 Redistributable (x64) is installed. Note that most linear and mixed-integer solvers must be installed (and licensed) separately, see the next section for details. The HeuristicLab.OrTools plugin is currently only available on 64-bit Windows.

Mixed-Integer (Linear) Programming (MIP, MILP)

OR-Tools contains a ​linear solver wrapper that can be used to define a MIP model once and solve it with a range of MIP solvers. Some solvers are already built into OR-Tools (BOP, Cbc, Clp, Glop) but for most solvers OR-Tools have to be built from source code, this version then has a dependency on the external solver. HeurisicLab includes a custom version of OR-Tools that allows users to simply install additional solvers without depending on them. Download the solvers here, they are free for academic use:

• ​CPLEX,
• ​Gurobi,
• ​GLPK (currently not supported by HeuristicLab) and
• ​SCIP.

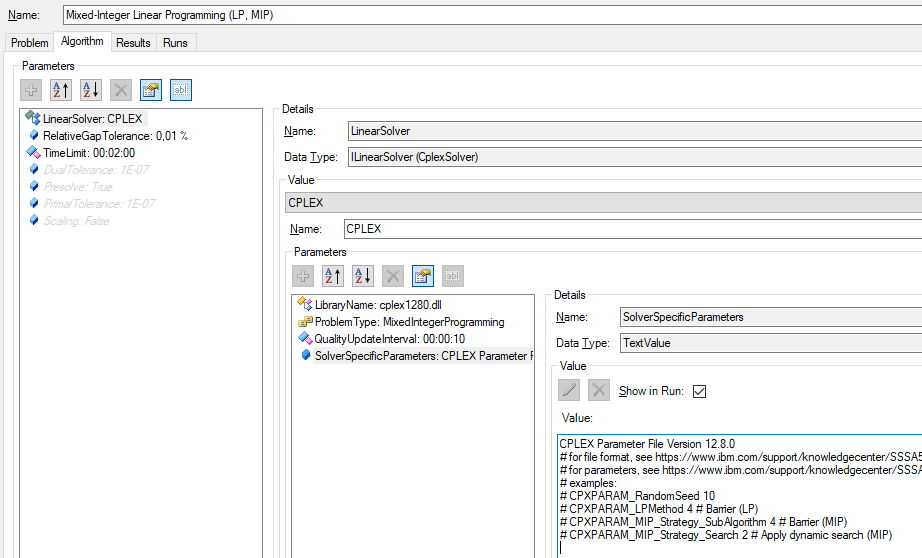
Make sure that the solver you install is added to the environment variable Path and the LibraryName property of the solver in the Algorithm view is set to the correct name of the solver DLL (e.g. cplex1280.dll for version 12.8.0 of CPLEX). The default values for the solver DLLs can be set in the configuration file of HeuristicLab. Note that most solvers offer to change the ProblemType property to LinearProgramming, the solver then solves the linear programming relaxation of your model (all integer constraints are removed).

For a general introduction to MIP and a simple model implemented using the linear solver wrapper, see ​https://developers.google.com/optimization/mip/integer_opt. For further examples demonstrating more advanced usage of the linear solver wrapper using the C# API, see ​https://github.com/google/or-tools/tree/master/examples/dotnet.

The HeuristicLab.ExactOptimization plugin provides a GUI for MIP, just create a new Mixed-Integer Linear Programming (LP, MIP) algorithm, found under Algorithms, Exact. You can either load your model from a file (MPS, Google OR-Tools Protocol Buffers files) or define your model using C# and directly accessing the linear solver wrapper. The next section shows the implementation of a Knapsack Problem (KSP) and a Traveling Salesman Problem (TSP).

Defining a MIP Model

A programmable MIP model requires you to implement the BuildModel method where you must define the decision variables, the constraints and the objective of your model. The Analyze method is used to retrieve the solution values of the decision variables, which can be added to the results to be accessible in the GUI. The Initialize method can be used for initialization.

Knapsack Problem (KSP)

The following MIP model can be pasted in HeuristicLab in the Problem tab of a Mixed-Integer Linear Programming (LP, MIP) algorithm. The Analyze method shows the definition of the ​0-1 Knapsack Problem. Note that you can drag any instance of a Knapsack Problem (KSP) to the variables list and rename it to Problem (remove the default problem first).

using System;
using System.Linq;
using System.Text;
using Google.OrTools.LinearSolver;
using HeuristicLab.Data;
using HeuristicLab.Encodings.BinaryVectorEncoding;
using HeuristicLab.ExactOptimization.LinearProgramming;
using HeuristicLab.Optimization;
using HeuristicLab.Problems.Knapsack;

public class KnapsackLinearModel : CompiledProblemDefinition, ILinearProblemDefinition {
  private Variable[] x;

  public override void Initialize() {
    if (vars.Contains("Problem"))
      return;
    vars["Problem"] = new KnapsackProblem();
  }

  public void BuildModel(Solver solver) {
    // Retrieve the problem data
    var W = vars.Problem.KnapsackCapacity.Value;
    IntArray weights = vars.Problem.Weights;
    IntArray values = vars.Problem.Values;
    // Define the decision variables
    x = solver.MakeBoolVarArray(values.Count());
    // Define the constraints
    solver.Add(weights.Select((w, i) => w * x[i]).ToArray().Sum() <= W);
    // Define the objective
    solver.Maximize(values.Select((v, i) => v * x[i]).ToArray().Sum());
  }

  public void Analyze(Solver solver, ResultCollection results) {
    // Retrieve the problem data
    var capacity = vars.Problem.KnapsackCapacity;
    var weights = vars.Problem.Weights;
    var values = vars.Problem.Values;
    // Retrieve the solution values of the objective and the decision variables
    var solution = new BinaryVector(x.Select(xi => xi.SolutionValue() == 1).ToArray());
    var quality = new DoubleValue(solver.Objective().Value());
    // Update the problem
    if (vars.Problem.BestKnownQuality == null || quality.Value > vars.Problem.BestKnownQuality.Value) { 
      vars.Problem.BestKnownSolution = solution;
      vars.Problem.BestKnownQuality = quality;
    }
    // Update the result
    results.AddOrUpdateResult("BestKnapsackSolution", new KnapsackSolution(solution, quality, capacity, weights, values));
  }
}

Traveling Salesman Problem (TSP)

The following MIP model can be pasted in HeuristicLab in the Problem tab of a Mixed-Integer Linear Programming (LP, MIP) algorithm. The Analyze method shows the definition of the ​Miller-Tucker-Zemlin formulation of the Traveling Salesman Problem. Note that you can drag any instance of a Traveling Salesman Problem (TSP) to the variables list and rename it to Problem (remove the default problem first).

using System;
using System.Collections.Generic;
using System.Linq;
using Google.OrTools.LinearSolver;
using HeuristicLab.Data;
using HeuristicLab.Encodings.PermutationEncoding;
using HeuristicLab.ExactOptimization.LinearProgramming;
using HeuristicLab.Optimization;
using HeuristicLab.Problems.TravelingSalesman;

using HeuristicLab.Problems.Instances;

public class TravelingSalesmanLinearModel : CompiledProblemDefinition, ILinearProblemDefinition {
  private Variable[,] x;

  public override void Initialize() {
    if (vars.Contains("Problem"))
      return;
    vars["Problem"] = new TravelingSalesmanProblem();
  }

  public void BuildModel(Solver solver) {
    // Miller-Tucker-Zemlin formulation
    TravelingSalesmanProblem problem = vars.Problem;
    CalculateDistanceMatrix(problem);   
    var c = problem.DistanceMatrix;
    var n = c.Rows;
    var N = Enumerable.Range(0, n).ToList();
    // Define the decision variables
    x = solver.MakeBoolVarArray(n, n);
    var u = solver.MakeNumVarArray(n, 0, n - 1);
    // Define the constraints
    foreach (var j in N) {
      solver.Add(N.Where(i => i != j).Select(i => x[i, j]).ToArray().Sum() == 1);
    }
    foreach (var i in N) {
      solver.Add(N.Where(j => j != i).Select(j => x[i, j]).ToArray().Sum() == 1);
    }
    for (var i = 1; i < n; i++) {
      for (var j = 1; j < n; j++) {
        solver.Add(u[i] - u[j] + n * x[i, j] <= n - 1);
      }
    }
    // Define the objective
    solver.Minimize(
      (from i in N
       from j in N
       where i != j
       select c[i, j] * x[i, j]
      ).ToArray().Sum()
    );
  }

  public void Analyze(Solver solver, ResultCollection results) {
    // Retrieve the problem data
    var coordinates = vars.Problem.Coordinates;
    // Retrieve the solution values of the objective and the decision variables
    var solution = new Permutation(PermutationTypes.RelativeUndirected, GetTour(x));
    var quality = new DoubleValue(solver.Objective().Value());
    // Update the problem
    if (vars.Problem.BestKnownQuality == null || quality.Value < vars.Problem.BestKnownQuality.Value) { 
      vars.Problem.BestKnownSolution = solution;
      vars.Problem.BestKnownQuality = quality;
    }
    // Update the result
    results.AddOrUpdateResult("Best TSP Solution", new PathTSPTour(coordinates, solution, quality));
  }
  
  private static int[] GetTour(Variable[,] x) {
    var n = x.GetLength(0);
    var tour = new List<int> { 0 };

    while (true) {
      for (var i = 0; i < n; i++) {
        if (x[tour.Last(), i].SolutionValue() > 0) {
          if (i == tour[0])
            return tour.ToArray();
          tour.Add(i);
          break;
        }
      }
    }
  }

  private static void CalculateDistanceMatrix(TravelingSalesmanProblem problem) {
    if (problem.DistanceMatrix != null)
      return;
    
    // calculate distance matrix
    var distanceMeasure = GetDistanceMeasure(problem.Evaluator);
    var coordinates = problem.Coordinates.CloneAsMatrix();
    
    if (coordinates == null)
      throw new InvalidOperationException("Neither a distance matrix nor coordinates were given.");
    
    var dimension = coordinates.GetLength(0);
    var distanceMatrix = new DistanceMatrix(DistanceHelper.GetDistanceMatrix(distanceMeasure, coordinates, null, dimension));
    problem.DistanceMatrix = (DistanceMatrix)distanceMatrix.AsReadOnly();
  }
  
  private static DistanceMeasure GetDistanceMeasure(ITSPEvaluator evaluator) {
    if (evaluator is TSPEuclideanPathEvaluator)
      return  DistanceMeasure.Euclidean;
    if (evaluator is TSPRoundedEuclideanPathEvaluator)
      return DistanceMeasure.RoundedEuclidean;
    if (evaluator is TSPUpperEuclideanPathEvaluator)
      return DistanceMeasure.UpperEuclidean;
    if (evaluator is TSPGeoPathEvaluator)
      return DistanceMeasure.Geo;
    throw new InvalidOperationException("Unknown distance measure.");
  }
}

Implementing New Models in HeuristicLab

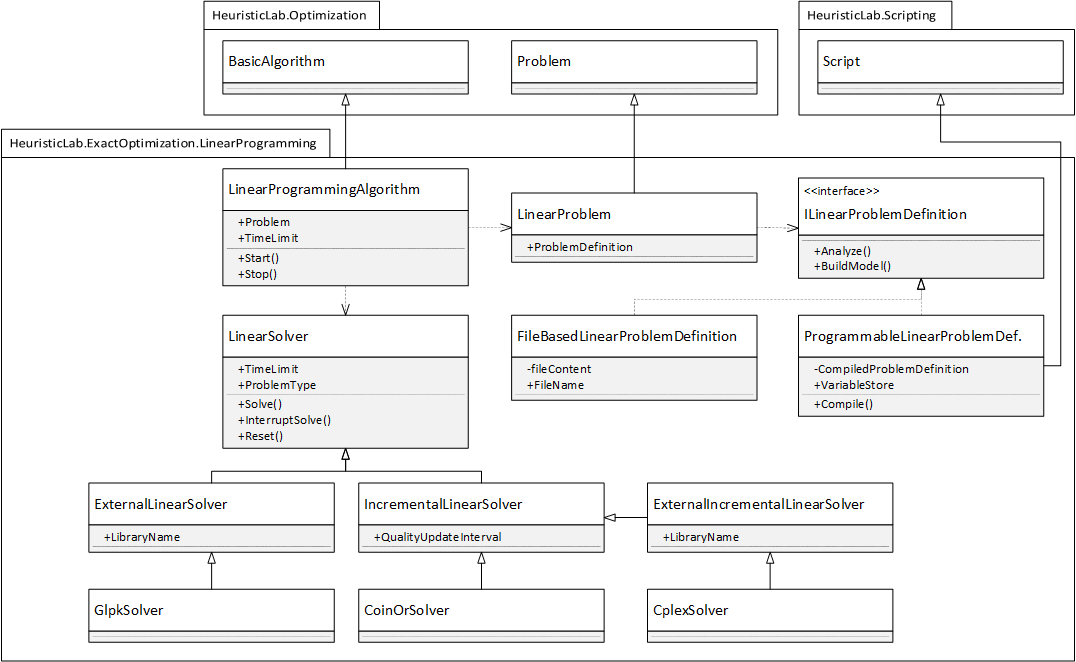
The class diagram below shows the simplified architecture of the HeuristicLab.ExactOptimization plugin. To implement a new model that can be easily accessed within HeuristicLab, implement the ILinearProblemDefintion interface.

The BuildModel method is used to define your model using the linear solver wrapper of OR-Tools, the Analyze method is used to retrieve the solution values of your decision variables. The following C# Script shows the implementation of the 0-1 Knapsack Problem (class KnapsackLinearModel), which is quite similar to the example script provided above, and the usage of this model (in the method Main) by solving it with all available solvers.

using System;
using System.Linq;
using Google.OrTools.LinearSolver;
using HeuristicLab.Common;
using HeuristicLab.Core;
using HeuristicLab.Data;
using HeuristicLab.Encodings.BinaryVectorEncoding;
using HeuristicLab.ExactOptimization.LinearProgramming;
using HeuristicLab.Optimization;
using HeuristicLab.Parameters;
using HeuristicLab.Persistence.Default.CompositeSerializers.Storable;
using HeuristicLab.Problems.Knapsack;
using Variable = Google.OrTools.LinearSolver.Variable;

public class KnapsackScript : HeuristicLab.Scripting.CSharpScriptBase {
  public override void Main() {
    var algorithm = new LinearProgrammingAlgorithm();
    vars.Algorithm = algorithm;
    algorithm.Problem.ProblemDefinition = new KnapsackLinearModel();
    
    foreach (var solver in algorithm.LinearSolverParameter.ValidValues) {
      Console.WriteLine("========== " + solver.Name + " ==========");
      
      algorithm.Prepare();
      algorithm.LinearSolver = solver;
      algorithm.Start();
      
      if (algorithm.Results.Any()) {
        algorithm.Results.ForEach(Console.WriteLine);
      } else {
        Console.WriteLine("Solver is not properly installed.");
      }
    }
    
    // you can also access the results afterwards, e.g.: 'algorithm.Runs.First().Results'    
  }

  [Item("Knapsack Linear Model", "Models a 0-1 knapsack problem.")]
  [StorableClass]
  public class KnapsackLinearModel : ParameterizedNamedItem, ILinearProblemDefinition {
  
    [Storable]
    private IValueParameter<KnapsackProblem> problemParam;
  
    private Variable[] x;
  
    public KnapsackLinearModel() {
      Parameters.Add(problemParam = new ValueParameter<KnapsackProblem>("Problem", new KnapsackProblem()));
    }
  
    private KnapsackLinearModel(KnapsackLinearModel original, Cloner cloner)
      : base(original, cloner) {
      problemParam = cloner.Clone(original.problemParam);
    }
  
    [StorableConstructor]
    private KnapsackLinearModel(bool deserializing) : base(deserializing) { }
  
    public KnapsackProblem Problem {
      get { return problemParam.Value; }
      set { problemParam.Value = value; }
    }
  
    public IValueParameter<KnapsackProblem> ProblemParameter {
      get { return problemParam; }
    }
  
    public void BuildModel(Solver solver) {
      // Retrieve the problem data
      var W = Problem.KnapsackCapacity.Value;
      var weights = Problem.Weights;
      var values = Problem.Values;
      // Define the decision variables
      x = solver.MakeBoolVarArray(values.Count());
      // Define the constraints
      solver.Add(weights.Select((w, i) => w * x[i]).ToArray().Sum() <= W);
      // Define the objective
      solver.Maximize(values.Select((v, i) => v * x[i]).ToArray().Sum());
    }
  
    public void Analyze(Solver solver, ResultCollection results) {
      // Retrieve the problem data
      var capacity = Problem.KnapsackCapacity;
      var weights = Problem.Weights;
      var values = Problem.Values;
      // Retrieve the solution values of the objective and the decision variables
      var solution = new BinaryVector(x.Select(xi => xi.SolutionValue() == 1).ToArray());
      var quality = new DoubleValue(solver.Objective().Value());
      // Update the problem
      if (Problem.BestKnownQuality == null || quality.Value > Problem.BestKnownQuality.Value) {
        Problem.BestKnownSolution = solution;
        Problem.BestKnownQuality = quality;
      }
      // Update the result
      results.AddOrUpdateResult("BestKnapsackSolution", new KnapsackSolution(solution, quality, capacity, weights, values));
    }
  
    public override IDeepCloneable Clone(Cloner cloner) {
      return new KnapsackLinearModel(this, cloner);
    }
  }
}