| Version 6 (modified by abeham, 10 years ago) (diff) |
|---|
How To Implement New VRP Problem Instances
Goals
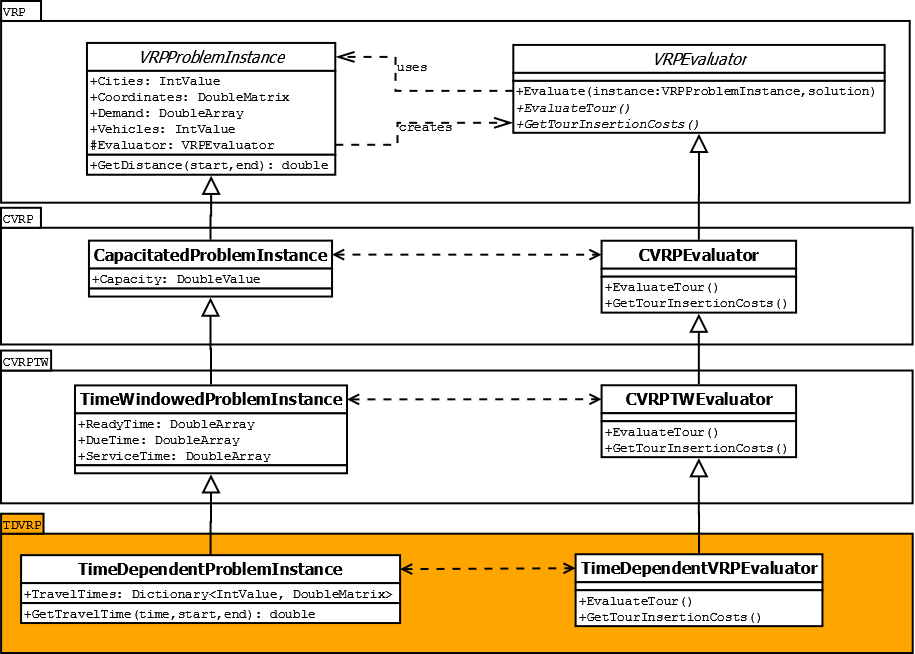
One way to implement a new VRP variant is by implementing a new VRPProblemInstance. This is a suitable possibility if the VRP variant requires additional model data. A VRPProblemInstance is responsible for storing all information about a VRP instance like coordinates, distances, demands, etc. By extending a VRPProblemInstance it is possible to add additional data as additional constraints or flexibility to a VRP variant. It is also necessary to implement a new VRPEvaluator (see the howto on implementing new VRP evaluators) to interpret the new data.
In addition to the new VRPProblemInstance a new parser for reading the additional data from a file is required. In order to integrate the new parser into HeuristicLab a VRPInstanceProvider and other components are also required.
After this tutorial you will be able to implement you own VRP variants that require additional model data. You will also have a basic understanding of the concepts and architecture concerning the VRPProblemInstance, the VRPInstanceProvider and related components.
The Time Dependent Vehicle Routing Problem
To show the procedure of implementing a new VRPProblemInstance, the implementation of the Time Dependent Travel Time Vehicle Routing Problem (TDVRP) is demonstrated. The TDVPR considers the travel time variation during a day.
In this tutorial, the TDVRP is based on the Capacitated Vehicle Routing Problem with Time Windows (CVRPTW). The additional data are the travel times, which associate a travel time factor for a specific time. There are multiple ways to assign the travel time to the VRP. One way is to specify a global function which maps a time of a day to a travel time for all connections, as shown the following figure (source).
In this tutorial we use travel-times matrices. Each matrix stores a travel time factor for every connection. Every travel time matrix also specifies a unique timestamp. Between the timestamp of a matrix and the subsequent matrix the travel times of the first matrix is used, resulting in hard steps of the travel time during the day.
Prerequisites
Before you start, make sure you have the latest version of the HeuristicLab source code ready. Then create a new plugin called HeuristicLab.TimeDependentVRP. For additional help for creating a new plugin, see the development center.
Your plugin need an additional dependency onto the HeuristicLab.Problems.VehicleRouting and the HeuristicLab.Problems.Instances.VehicleRouting plugin. The plugin should look like this:
[Plugin("HeuristicLab.TimeDependentVRP", "1.0.0.0")]
[PluginFile("HeuristicLab.TimeDependentVRP.dll", PluginFileType.Assembly)]
[PluginDependency("HeuristicLab.Problems.VehicleRouting", "3.4")]
[PluginDependency("HeuristicLab.Problems.Instances.VehicleRouting", "3.4")]
public class TimeDependentVRPPlugin : PluginBase {
}
In addition you will need references onto following HeuristicLab assemblies:
- HeuristicLab.Collections
- HeuristicLab.Common
- HeuristicLab.Core
- HeuristicLab.Data
- HeuristicLab.Operators
- HeuristicLab.Optimization
- HeuristicLab.Parameters
- HeuristicLab.Persistence
- HeuristicLab.Problems.VehicleRouting
- HeuristicLab.Problems.Instances
- HeuristicLab.Problems.Instances.VehicleRouting
ProblemInstance
Foundations
A VRPProblemInstance contains all data for a specific VRP problem, for example the number of cities, their coordinates and demands. In addition the VRPProblemInstance provides methods for calculate the distance between two cities. Internally a distance matrix is created beforehand for a fast calculation.
A VRPEvaluator uses the VRPProblemInstance and a solution candidate for the VRPProblemInstance to evaluate the solution candidate.
HeuristicLab implements several common VRP variants like the Capaciated VRP (CVRP) and VRP with Time Windows (VRPTW). Every VRP variant extends an existing VRPProblemInstance and adds the new data, for example the capacity for the vehicles in the CVRP. In order to interpret the new data a new VRPEvaluator for each VRPProblemInstance is also necessary.
Extending ProblemInstance and Evaluator
To implement a new VRP variant with additional model data you have to extend an existing VRPProblemInstance and VRPEvaluator. For this tutorial we extend the available CVRPTW.
Implement new ProblemInstance
The new TimeDependentProblemInstance derives from the existing TimeWindowedProblemInstance. In addition we store the travel times as dictionary of a timestamp and the travel time matrix. We also specify a method for determining the travel time between two cities for a specific time.
public interface ITimeDependentProblemInstance : IVRPProblemInstance {
ItemDictionary<IntValue, DoubleMatrix> TravelTimes { get; }
double GetTravelTime(double time, int x, int y);
}
To implement the TimeDependentProblemInstance in HeuristicLab you have to add specific code for cloning and persistence.
[Item("TimeDependentProblemInstance", "Represents a time dependant CVRPTW instance.")]
[StorableClass]
public class TimeDependentProblemInstance
: CVRPTWProblemInstance, ITimeDependentProblemInstance {
[StorableConstructor]
protected TimeDependentProblemInstance(bool deserializing) : base(deserializing) { }
public override IDeepCloneable Clone(Cloner cloner) {
return new TimeDependentProblemInstance(this, cloner);
}
protected TimeDependentProblemInstance(TimeDependentProblemInstance original, Cloner cloner)
: base(original, cloner) {
AttachEventHandlers();
}
[StorableHook(HookType.AfterDeserialization)]
private void AfterDeserialization() {
AttachEventHandlers();
}
}
To store the dictionary of timestamps and travel time matrices we use a ValueParameter. Furthermore we need to register an event handler to the parameter. If the travel times change we have to re-evaluate our known solution. To link the new VRPProblemInstance to a new VRPEvaluator we have to override the Evaluator property and return our new TimeDependentVRPEvaluator.
public class TimeDependentProblemInstance
: CVRPTWProblemInstance, ITimeDependentProblemInstance {
protected IValueParameter<ItemDictionary<IntValue, DoubleMatrix>> TravelTimesParameter {
get { return (IValueParameter<ItemDictionary<IntValue, DoubleMatrix>>)Parameters["TravelTimes"]; }
}
public ItemDictionary<IntValue, DoubleMatrix> TravelTimes {
get { return TravelTimesParameter.Value; }
set { TravelTimesParameter.Value = value; }
}
public TimeDependentProblemInstance() {
Parameters.Add(new ValueParameter<ItemDictionary<IntValue, DoubleMatrix>>("TravelTimes", "The time dependent travel times.",
new ItemDictionary<IntValue, DoubleMatrix>()));
AttachEventHandlers();
}
private void AttachEventHandlers() {
TravelTimesParameter.ValueChanged += TravelTimesParameterOnValueChanged;
}
private void TravelTimesParameterOnValueChanged(object sender, EventArgs eventArgs) {
EvalBestKnownSolution();
}
protected override IVRPEvaluator Evaluator {
get { return new TimeDependentVRPEvaluator(); }
}
}
The GetTravelTime method is used for determining the travel time between two cities for a given time by first determining the timestamp key for the dictionary. This is done by finding the highest timestamp in the keys that is smaller than the given time.
public double GetTravelTime(double time, int x, int y) {
double travelTime = 1;
if (TravelTimes != null) {
var sortedKeys = TravelTimes.Keys.OrderBy(k => k.Value).ToList();
int i = 0;
IntValue key = null;
while (i < sortedKeys.Count && sortedKeys[i].Value <= time) {
key = sortedKeys[i];
i++;
}
if (key != null)
travelTime = TravelTimes[key][x, y];
}
return travelTime;
}
Implement new Evaluator
In order to make use of the travel time a new VRPEvaluator is necessary. For detailed information about how to implement a new VRP Evaluator, see the howto on implementing new VRP evaluators. As we derived from CVRPTWProblemInstance for the new TimeDependentProblemIntance, we now derive the TimeDependentVRPEvaluator from the existing CVRPTWEvaluator.
[Item("TimeDependentVRPEvaluator", "Represents a time dependent VRP evaluator.")]
[StorableClass]
public class TimeDependentVRPEvaluator
: CVRPTWEvaluator {
[StorableConstructor]
protected TimeDependentVRPEvaluator(bool deserializing) : base(deserializing) { }
public TimeDependentVRPEvaluator() {
}
public override IDeepCloneable Clone(Cloner cloner) {
return new TimeDependentVRPEvaluator(this, cloner);
}
protected TimeDependentVRPEvaluator(TimeDependentVRPEvaluator original, Cloner cloner)
: base(original, cloner) {
}
}
EvaluateTour
Note: Because the evaluator is called very frequently in the optimization progress, the performance is critical. Therefore the design favors speed over proper architecture and code duplication is accepted.
For the EvaluateTour method we copy the existing implementation from the base class. The only thing we need to do is to multiply the driven distance with the travel time. This is done by following changes in the method. First get the TimeDependentProblemInstance in the beginning of the method by casting the available problem instance.
ITimeDependentProblemInstance ttvrp = instance as ITimeDependentProblemInstance;
In the center of the method change the line
double currentDistace = vrptw.GetDistance(start, end, solution);
to
double currentDistace = vrptw.GetDistance(start, end, solution) * ttvrp.GetTravelTime(time, start, end);
After these changes the travel time is applied to every driven distance.
GetTourInsertionCosts
Unfortunately the increment based evaluation is trickier than the evaluation of a whole tour. Because the insertion of a stop can cause different travel times for the following stops the existing implementation cannot be used directly.
For simplicity and reducing the scope of this tutorial we evaluate the whole tour and calculate the quality difference. Of course this is increases the runtime drastically, but we want to focus on other topics in this tutorial.
protected override double GetTourInsertionCosts(IVRPProblemInstance instance, IVRPEncoding solution, TourInsertionInfo tourInsertionInfo, int index, int customer, out bool feasible) {
TourEncoding individual = null;
if (solution is TourEncoding)
individual = solution as TourEncoding;
else {
individual = PotvinEncoding.ConvertFrom(solution, instance);
}
int tourIdx = -1;
for (int i = 0; i < individual.Tours.Count; i++) {
if (solution.GetVehicleAssignment(i) == tourInsertionInfo.Vehicle)
tourIdx = i;
}
Tour tour = individual.Tours[tourIdx];
tour.Stops.Insert(index, customer);
VRPEvaluation newEval = instance.EvaluateTour(tour, individual);
tour.Stops.RemoveAt(index);
feasible = instance.Feasible(newEval);
return newEval.Quality - tourInsertionInfo.Quality;
}
Read, provide and interpret Data
After the previous section we can use the new problem instances of the Time Dependent VRP variant and evaluate them. However, we need to create the problem instances first. For a brief overview the following sequence diagram shows how the data flows between the different components in the creation process. For simplicity more complex HeuristicLab components are abstracted.
Parser
The first step is to read all relevant data from a file. Our parser is based on the existing SolomonParser. Unfortunately the parser is not designed for reusability, therefore we have to copy the implementation and modify it.
First, we create a new class TimeDependentParser and copy the fields and methods from the SolomonParser. Then we add our new data, the travel times, to the class.
//new data
private Dictionary<int, double[,]> travelTimes;
public Dictionary<int, double[,]> TravelTimes {
get {
return travelTimes;
}
}
public TimeDependentParser() {
...
travelTimes = new Dictionary<int, double[,]>();
}
In the parse method we additionally have to read all values from the travel time matrices and store them in the dictionary.
public void Parse() {
...
// read matrices
while (line != null) {
if (line == "TIME MATRIX") {
line = reader.ReadLine();
int time = int.Parse(line);
travelTimes[time] = new double[cities, cities];
for (int i = 0; i < cities; i++) {
line = reader.ReadLine();
string[] tokens = line.Split('\t');
for (int j = 0; j < cities; j++) {
travelTimes[time][i, j] = double.Parse(tokens[j], CultureInfo.InvariantCulture);
}
}
}
line = reader.ReadLine();
}
}
}
InstanceProvider
To provide a problem with a problem instance, HeuristicLab uses a ProblemInstanceProvider. A ProblemInstanceProvider specifies methods for loading the problem instance data from a source (a Stream or File) or provides problem instances by itself (from a preconfigured data store). The loading procedure from a file is handled by our TimeDependentParser from the previous section; we simply have to call it.
The InstanceProvider returns problem unspecific data because some data can be imported from different problems. For example the traveling salesman data can be imported by the traveling salesman problem and the quadratic assignment problem. For the problem unspecific data we create a TimeDependentData which derives from the existing CVRPTWData and add the dictionary with the timestamps and travel times.
public class TimeDependentData : CVRPTWData {
public Dictionary<int, double[,]> TravelTimes { get; set; }
}
An abstract implementation of the ProblemInstanceProvider for VRP is the VRPInstanceProvider}}. We only have to override certain methods for the data import. The {{{ImportData and LoadData method both use the TimeDependentParser to parse the file. First we create a new TimeDependentInstanceProvider class which derives from the existing VRPInstanceProvider and override a few methods. In the LoadInstance method we call the parser and copy the loaded values from the parser to the TimeDependentData object.
public class TimeDependentInstanceProvider
: VRPInstanceProvider {
public override string Name {
get { return "Time Dependent VRP"; }
}
public override string Description {
get { return "Benchmark test set"; }
}
public override Uri WebLink {
get { return null; }
}
public override string ReferencePublication {
get { return string.Empty; }
}
protected override string FileName {
get { return "TDVRP"; }
}
public override bool CanImportData {
get { return true; }
}
public override VRPData ImportData(string path) {
return LoadInstance(new TimeDependentParser(path));
}
protected override VRPData LoadData(Stream stream) {
return LoadInstance(new TimeDependentParser(stream));
}
private TimeDependentData LoadInstance(TimeDependentParser parser) {
parser.Parse();
var instance = new TimeDependentData {
Dimension = parser.Cities + 1,
Coordinates = parser.Coordinates,
Capacity = parser.Capacity,
Demands = parser.Demands,
DistanceMeasure = DistanceMeasure.Euclidean,
ReadyTimes = parser.Readytimes,
ServiceTimes = parser.Servicetimes,
DueTimes = parser.Duetimes,
MaximumVehicles = parser.Vehicles,
Name = parser.ProblemName,
TravelTimes = parser.TravelTimes
};
return instance;
}
}
Interpreter
To link the problem neutral data to the problem specific instance a ProblemInstanceConsumer is used. The VehicleRoutingProblem itself is a consumer of VRPData and specifies a Load method. To determine which problem specific instance has to be created, a lookup for a VRPDataInterpreter is performed. The VRPDataInterpreter is then responsible for transferring the problem independent data to the problem specific instance.
For the Time Dependent VRP variant we create a TimeDependentInterpreter which derives from the CVRPTWInterpreter. The Interpret method first calls the implementation from the base class to copy the CVRPTW data and copy the travel times to the problem instance itself.
class TimeDependentInterpreter : CVRPTWInterpreter, IVRPDataInterpreter<TimeDependentData> {
protected override IVRPProblemInstance CreateProblemInstance() {
return new TimeDependentProblemInstance();
}
protected override void Interpret(IVRPData data, IVRPProblemInstance problemInstance) {
base.Interpret(data, problemInstance);
TimeDependentData ttData = (TimeDependentData)data;
TimeDependentProblemInstance problem = (TimeDependentProblemInstance)problemInstance;
var travelTimes = new ItemDictionary<IntValue, DoubleMatrix>();
foreach (var key in ttData.TravelTimes.Keys) {
travelTimes[new IntValue(key)] = new DoubleMatrix(ttData.TravelTimes[key]);
}
problem.TravelTimes = travelTimes;
}
}
Result
To load and start the time dependent VRP variant in HeuristicLab, we first need a valid file to load the TimeDependentData from. We use the data from the Solomon(CVRPTW) instance C101 and add the travel time matrices (dimension must match number of cities). For the travel times random values between 0.5 and 1.0 has been generated. The file should look like this:
C101
VEHICLE
NUMBER CAPACITY
25 200
CUSTOMER
CUST NO. XCOORD. YCOORD. DEMAND READY TIME DUE DATE SERVICE TIME
0 40 50 0 0 1236 0
1 45 68 10 912 967 90
2 45 70 30 825 870 90
3 42 66 10 65 146 90
4 42 68 10 727 782 90
...
TIME MATRIX
0
0.925768957 0.520976414 0.562468007 0.750021875 0.61487113 ...
0.969856182 0.953186691 0.793840100 0.849949851 0.722734144 ...
0.686240672 0.770091988 0.76052254 0.943715274 0.831277119 ...
0.677805486 0.568948045 0.52780747 0.597541347 0.801783863 ...
0.890418577 0.827736775 0.596248865 0.900999375 0.913970905 ...
...
TIME MATRIX
200
0.705789629 0.57992851 0.567098964 0.607691814 0.726458799 ...
0.889918297 0.914455074 0.665679621 0.889941709 0.656366975 ...
0.647343773 0.526871001 0.94999237 0.82489978 0.591413065 ...
0.899079133 0.971614305 0.612777292 0.740562405 0.773627941 ...
0.519786836 0.914662095 0.905892404 0.963831082 0.598044971 ...
...
We simply load the data by first opening one of the VRP samples, e.g. the Tabu Search – VRP sample. At the Library we choose our TimeDependent VRP implementation, and open our modified data file (c101_TT.txt from the attachments). In the Tabu Search Parameters tab we set the MoveGenerator to PotvinPDShiftMultiMoveGenerator. Optionally set the SolutionCreator to PushForwardInsertionCreator in the Problem tab. Finally run the algorithm.
As you can see, the result differs slightly compared to the original version without time dependent travel times. Apparently the change is favorable because the travel time can be used optimal for the additional stops.
Attachments (7)
- 1_TDVRP_travel_time.png (7.6 KB) - added by pfleck 11 years ago.
- 2_TDVRP_ProblemInstance_simple.png (13.3 KB) - added by pfleck 11 years ago.
- 3_TDVRP_ProblemInstance_full.png (41.8 KB) - added by pfleck 11 years ago.
- 4_TDVRP_DataFlow.png (29.1 KB) - added by pfleck 11 years ago.
- 5_TDVRP_Result.png (14.5 KB) - added by pfleck 11 years ago.
- c101_TT.txt (718.5 KB) - added by pfleck 11 years ago.
- HeuristicLab.TimeDependentVRP.zip (18.3 KB) - added by pfleck 10 years ago.
Download all attachments as: .zip